

/简体/

/简体/
/英文/
/简体/
/简体/

/简体/

/简体/
/简体/

/简体/

/简体/
软件Tags:
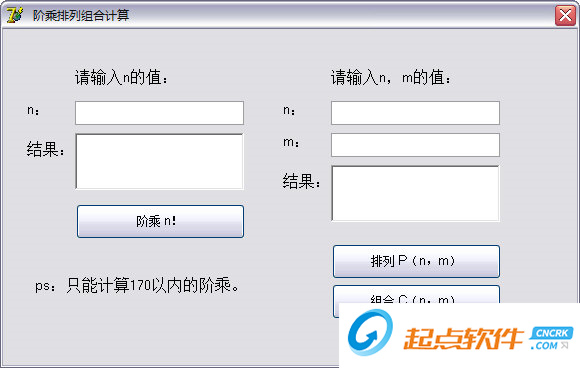
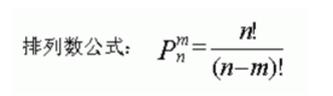
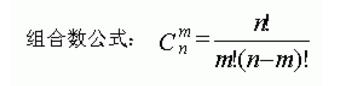

 指间计算器 v1.0免费版计算器软件 / 1.2M
指间计算器 v1.0免费版计算器软件 / 1.2M
 文件哈希值批量计算器 v1.0.3免费版计算器软件 / 36KB
文件哈希值批量计算器 v1.0.3免费版计算器软件 / 36KB
 Qalculate v4.4官方版计算器软件 / 78.8M
Qalculate v4.4官方版计算器软件 / 78.8M
 阿贵股票计算器 v2.0.0.0计算器软件 / 679KB
阿贵股票计算器 v2.0.0.0计算器软件 / 679KB
 MSICtorJME多功能计算器 v1.0a免费版计算器软件 / 27.0M
MSICtorJME多功能计算器 v1.0a免费版计算器软件 / 27.0M
 Localc v1.0免费版计算器软件 / 3.9M
Localc v1.0免费版计算器软件 / 3.9M
 卡方检验计算器 v3.7.78官方版计算器软件 / 4M
卡方检验计算器 v3.7.78官方版计算器软件 / 4M
 GeoGebra CAS计算器 v6.0.794.0官方版计算器软件 / 94.1M
GeoGebra CAS计算器 v6.0.794.0官方版计算器软件 / 94.1M
 补仓计算器 v1.0免费版计算器软件 / 10.1M
补仓计算器 v1.0免费版计算器软件 / 10.1M
 文件唯一识别码计算工具 v1.0免费版计算器软件 / 10.2M
文件唯一识别码计算工具 v1.0免费版计算器软件 / 10.2M